SANJITA SRINATH

What’s so special about 3? It’s known as the perfect number: harmony, wisdom, understanding. But what about mathematically? Let’s play a numbers game and find out.

Alright here’s game 1. Let’s play rock paper scissors with numbers. We have 5 options: 1, 2, 3, 4, and 5. We each choose 1. My number is my base and your number is my exponent and vice versa. Highest number wins. Here’s an example. I’ll choose 2. You can have 4. Therefore my number is 2^4 and your’s is 4^2. Would you look at that? We tied! Take a couple tries with the people around you and once you’re done, take a look at the image below for a cheat sheet.

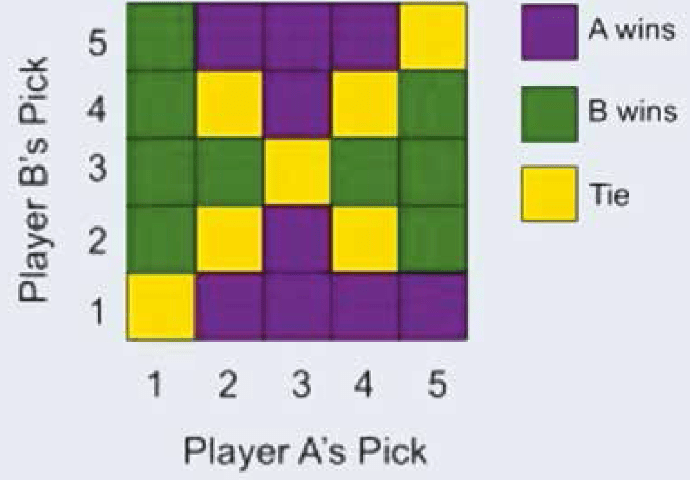
Ok… Let’s expand this game to 10 options: 1, 2, 3, 4, 5, 6, 7, 8, 9 & 10. Let’s also place bets on which numbers gonna win. I’ll place $3 on 3.

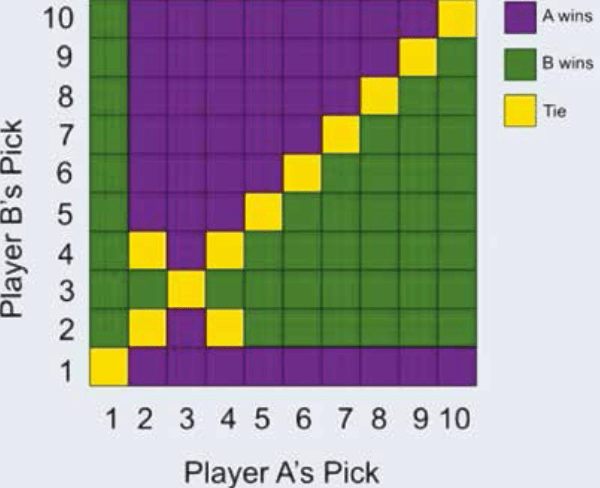
And would you look at that. 3 wins yet again. So what’s so special about 3? What would happen if we make our game bigger, and bigger, and bigger?

Let’s make it mathy. So, you’ve probably clued in by now that this may or may not be an optimization problem. Suppose Player A chooses k and Player B chooses x, this means that Player A wins whenever k^x-x^k>0. Therefore, Player A wants to maximize k^x-x^k.

Let’s make this an implicit equation to better represent the situation. Let’s call it y^x = x^y.

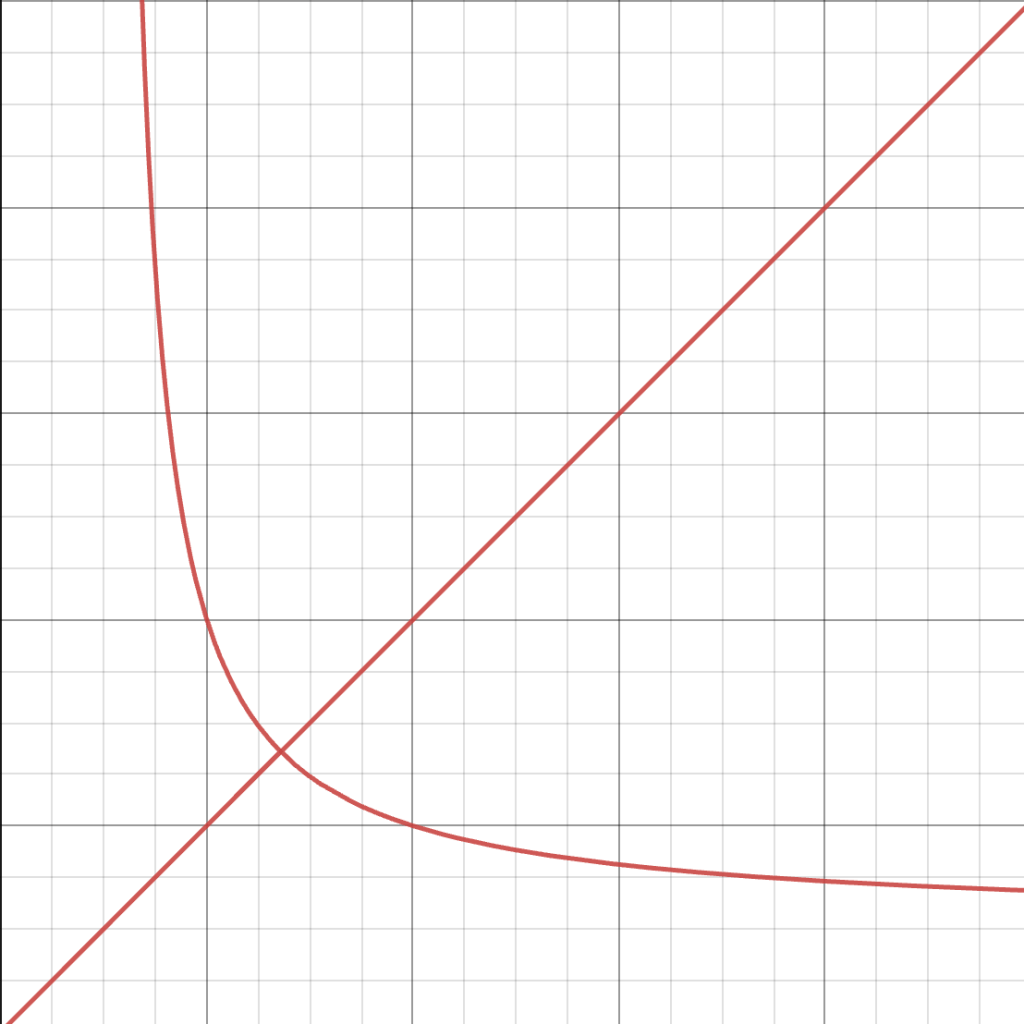
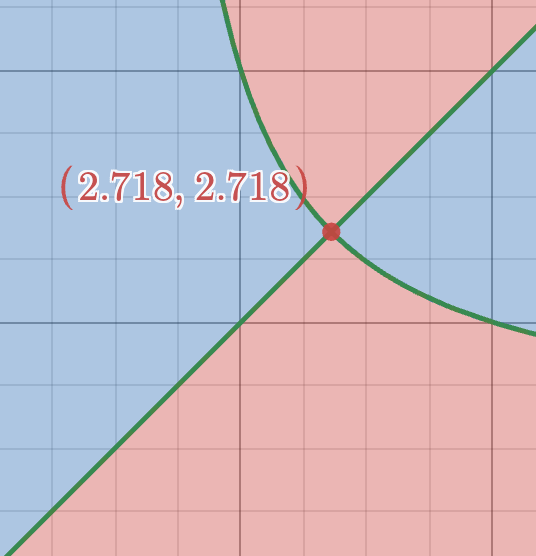
Alright, this is our curve. Does it look familiar? Let’s put a couple shaded areas on here to make it easier to look at. Let’s add the areas x^y>y^x and y^x>x^y.

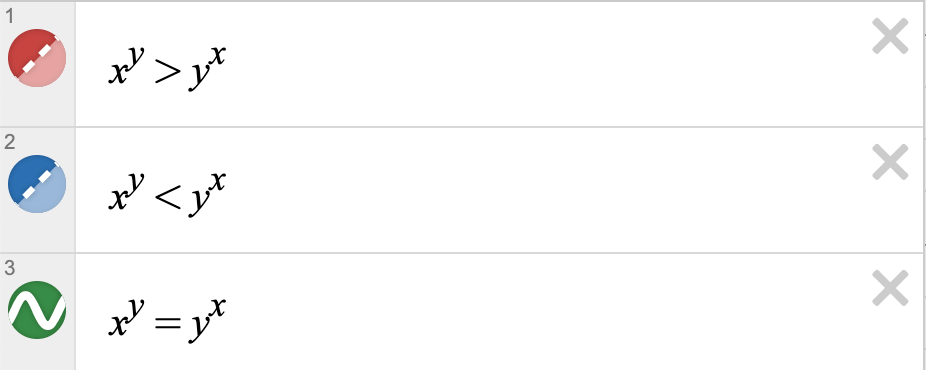
Alright so it’s evident to see in the red areas, player “X” wins and in the blue area, player “Y” wins. So now, we gotta find exactly what that intersection point is. Let’s take a random guess. It’s gonna be somewhere close to 3.

Alright, so we’re somewhat close to 3. Let’s try to narrow it down a bit further. Now my title may have given you a spoiler but let’s reach it mathematically.

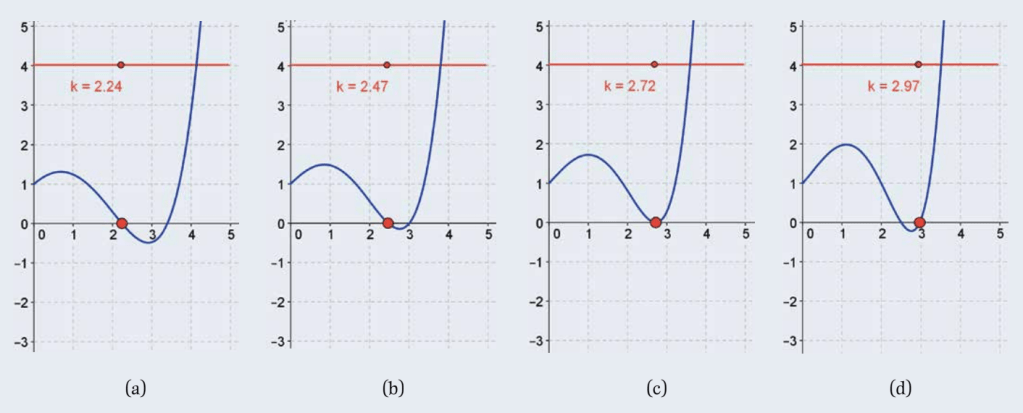
Let’s switch back to the maximization equation from earlier. Let’s graph h(x) = k^x-x^k, using k as a slider. We can see that for any value of k, there are usually 2 roots, unless it’s e, and then we have one root and it’s a minimum. What does this mean?

This means that when k=e, h(x) is always equal to or above 0, meaning that Player A who chooses k will either always win or tie.

So there’s a series of complicated equations we can go through to kindddddd offfff solve it, but let’s skip those and use e as a reasonable guess. And guess what, plotting (e,e) gives us a pretty reasonable spot.